Question

A wire with a resistance of 5.3 ω is drawn out through a die so that its new length is 4 times its original length. find the resistance of the longer wire, assuming that the resistivity and density of the material are unchanged.

Answer 1

Since resistance is based on cross-sectional area, the new wire would be thinner and its resistance will go up. Neglecting any change to the atomic structure of the wire, and a constant volume over the stretching, the cross section would be reduced by 4 times and its resistance would go up 4 times to 21.2 Ohms

Answer 2

The resistance of a wire is defined as
R = (ρL)/A
where
ρ = resistivity
L = length
A = cross-sectional area

Before the wire is drawn, let
L₁ = the length
A₁ = the cross-sectional area.

The volume of the wire and its resistivity remain unchanged after it is drawn.
After it is drawn, the new length is
L₂ = 4L₁
To preserve the volume, the new cross-sectional area is
A₂ = (L₁A₁)/L₂ = (L₁A₁)/(4L₁) = A₁/4

The initial resistance is given as
R₁ = (ρL₁)/A₁ = 5.3 Ω

The final resistance is

`R_(2)= (\rho L_(2))/(A_(2)) = (\rho (4L_(1)))/(A_(1)/4) = 16 ((\rho L_(1))/(A_(1))) = 16*5.3 \, \Omega = 84.8 \, \Omega`

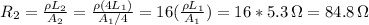
Answer: 84.8 Ω