Question

A particle moves along the curve below. y = 24 + x3 as it reaches the point (1, 5), the y-coordinate is increasing at a rate of 4 cm/s. how fast is the x-coordinate of the point changing at that instant?

Answer 1

To find the rate of change of the x-coordinate at the point (1, 5) with a given y-coordinate rate of change, we use the chain rule to differentiate the equation y = 24 +
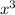`x^3` with respect to time, and solve for dx/dt.

Step-by-step explanation:

The student's question involves the relationship between the rates of change of the x-coordinate and y-coordinate of a particle moving along a curve. Given the equation y = 24 +
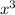`x^3`, we need to find how fast the x-coordinate is changing at the point (1, 5), given that the y-coordinate is increasing at a rate of 4 cm/s. To find this, we can use the chain rule from calculus to relate the rates of change. Differentiating both sides with respect to time t, we get dy/dt = 3
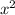`x^2` dx/dt. Solving for dx/dt, we find the rate of change of the x-coordinate when x = 1 and dy/dt = 4 cm/s.