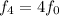Question

A satellite revolves around a planet at an altitude equal to the radius of the planet. the force of gravitational interaction between the satellite and the planet is f0. then the satellite is brought back to the surface of the planet. find the new force of gravitational interaction f4. express your answer in terms of f0.

Answer 1

f4 is 4 times larger than f0 The force of gravity between two masses is F = G M1M2/r^2 where F = Force G = Gravitational constant M1 = Mass of object 1 M2 = Mass of object 2 r = distance between the center of masses of the objects. So in the first case, the satellite is at an altitude of r above the surface. But it's really at a distance of 2r from the center of mass of the planet. And in the second case, the situation is that it's at distance r from the center of mass of the planet. So we have: f0 = G M1M2/((2r)^2) = G M1M2/(4r^2) and f4 = G M1M2/r^2 Let's divide f4 by f0 (G M1M2/r^2) / G M1M2/(4r^2) = (G M1M2/r^2) * (4r^2)/(G M1M2) = (1/r^2) * (4r^2)/1 = (4r^2)/r^2 = 4/1 = 4 So f4 = f0 * 4

Answer 2

Let
M = the mass of the planet
n = the mass of the satellite.
r = the radius of the planet

When the satellite is at a distance r from the surface of the planet, the distance between the centers of the two masses is 2r.
The gravitational force between them is

`f_(0) = (GMm)/((2r)^(2)) = (1)/(4) ( (GMm)/(r^(2)) )`
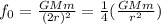
where
G = the gravitational constant.

When the satellite is on the surface of the planet, the distance between the two masses is r.
The gravitational force between them is

`f_(4) = (GMm)/(r^(2)) =4f_(0)`

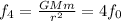
Answer:
`f_(4) = 4f_(0)`