Question

What are the x and y intercepts of the linear function represented in the table?

Answer 1

First, get the slope m, using any of the two ordered pairs in the table. For this problem we will use (2,10) and (3,12).

The slope of a linear function can defined using two points by

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ \\ \text{Given:} \\ (2,10)\rightarrow(x_1,y_1) \\ (3,12)\rightarrow(x_2,y_2) \\ \\ \text{Substitute the values and we get} \\ m=(y_2-y_1)/(x_2-x_1) \\ m=(12-10)/(3-2) \\ m=(2)/(1) \\ m=2 \end{gathered}`

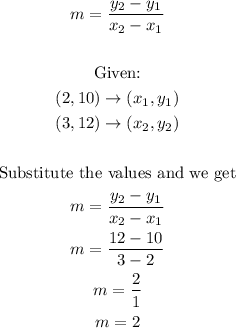
Now that we have the slope, we will solve for the y-intercept by using the y-intercept form of a linera function. We use any of the three points in the table, for this case we will use (4,14).

The y-intercept form of a linear function is defined as

`\begin{gathered} y=mx+b \\ \text{where} \\ m\text{ is the slope} \\ b\text{ is the y-intercept} \\ \\ \text{Given:} \\ (4,14)\rightarrow(x,y) \\ m=2 \\ \\ y=mx+b \\ 14=(2)(4)+b \\ 14=8+b \\ 14-8=b \\ 6=b \\ b=6 \\ \\ \text{Therefore, the y-intercept is 6} \end{gathered}`

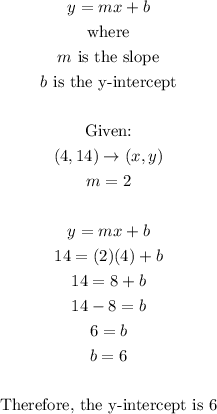
To solve for the x-intercept, we set y = 0 to our linear function

`\begin{gathered} y=mx+b \\ y=2x+6 \\ 0=2x+6 \\ -6=2x \\ 2x=-6 \\ (2x)/(2)=(-6)/(2) \\ x=-3 \\ \\ \text{therefore, the x-intercept is -3} \end{gathered}`

Summary, therefore the x and y intercepts of the linear function y = 2x+6 is (-3,0) and (0,6).