Consider this geometric sequence.
1, 2, 4, 8, ...
By considering the ratio between the first and the second, and the second and the third, we can begin to see that it has an equal ratio of 2.
Using the geometric sequence formula:
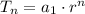
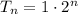
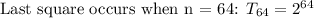
This means there will be 2^64 grains on the last square.