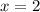The values are as follows:
-
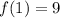
- If
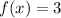 , then
, then

-
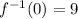
- If
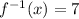 , then
, then
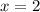
The provided image shows a function
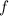 with a set of inputs (x values) and their corresponding outputs (f(x) values). To answer the questions, we need to use the given function values and apply the concept of a one-to-one function, which, by definition, has a unique output for every unique input and vice versa.
with a set of inputs (x values) and their corresponding outputs (f(x) values). To answer the questions, we need to use the given function values and apply the concept of a one-to-one function, which, by definition, has a unique output for every unique input and vice versa.
Here are the steps to find the required values:
1.
 Find the output when the input
Find the output when the input
 is 1.
is 1.
2. If
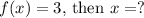 : Find the input that gives an output of 3.
: Find the input that gives an output of 3.
3.
 : Find the input that corresponds to an output of 0, which is the inverse function value.
: Find the input that corresponds to an output of 0, which is the inverse function value.
4. If
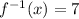 , then
, then
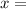 ?: Find the output which, when passed through the inverse function, gives an input of 7.
?: Find the output which, when passed through the inverse function, gives an input of 7.
Let's calculate these step by step.
Here are the detailed calculations for the given function:
1. To find
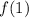 , we look at the value of the function when the input
, we look at the value of the function when the input
 is 1. The output is 9.
is 1. The output is 9.
2. To find the input
 such that
such that
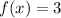 , we look for the input value that corresponds to the output of 3. This input value is 6.
, we look for the input value that corresponds to the output of 3. This input value is 6.
3. To find
 , we look for the input value that corresponds to the output of 0. Since the function is one-to-one, the inverse function
, we look for the input value that corresponds to the output of 0. Since the function is one-to-one, the inverse function
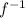 will give us the original input for this output, which is 9.
will give us the original input for this output, which is 9.
4. To find
 such that
such that
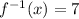 , we need to find the output
, we need to find the output
 which, when passed through the inverse function, gives an input of 7. Since
which, when passed through the inverse function, gives an input of 7. Since
 , then
, then
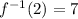 , so
, so
 is 2.
is 2.
So the values are as follows:
-
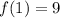
- If
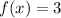 , then
, then

-
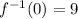
- If
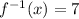 , then
, then