Question

Which inequality is equivalent to 
`3+ (4)/(x) \geq (x+2)/(x)` ?

A 
`(2x+2)/(x) \geq 0`
B 
`(2x+6)/(x) \geq 0`
C
`(-x+5)/(x) \geq 0`
D
`(-x+9)/(x) \geq 0`

Please show work and explain. I legitimately want to understand how to solve a question like this. Thank you!

Answer 1

First, take all expressions to one side of the inequality:


`\displaystyle{ 3+(4)/(x)- (x+2)/(x) \geq 0`.

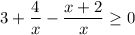
Multiply 3 by
`\displaystyle{ (x)/(x)` to write it as a fraction with denominator equal to the other expressions


`\displaystyle{ (3x)/(x)+(4)/(x)- (x+2)/(x) \geq 0`.


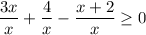
Since all three expressions have equal denominator, we collect them into one rational expression as follows:


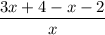
`\displaystyle{ (3x+4-x-2)/(x)`, which is equal to
`\displaystyle{ (2x+2)/(x)`.


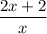
Thus the inequality is
`\displaystyle{ (2x+2)/(x) \geq 0`.


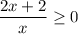
Answer: A