Answer:
(A)
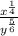
Explanation:
The given expression is:
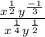
Upon solving the given expression, we get
=
 (using the property of exponents and powers that if base is same then the powers gets added.)
(using the property of exponents and powers that if base is same then the powers gets added.)
=
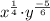
=
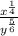
which is the required simplified form of the given equation.
Hence, option A is correct.