2 Answers

Melekes · Answer 1 · 2018-02-03T05:14:21+0000

10x + 16 ≥ 6x + 20
Subtract both sides by 16
10x ≥ 6x + 4
Subtract both sides by 6x
4x ≥ 4
Divide both sides by 4
x ≥ 1
Have an awesome day! :)

RomkaLTU · Answer 2 · 2018-02-07T22:03:02+0000

Answer:

The solution of given inequality is x ≥1.

Explanation:

The given inequality is

$10x+16\geq 6x+20$

We need to separate the variable terms to solve the above inequality.

Subtract 6x and 16 from both sides to separate the variables on left side.

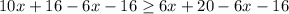
$10x+16-6x-16\geq 6x+20-6x-16$

On combining like terms we get

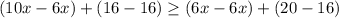
$(10x-6x)+(16-16)\geq (6x-6x)+(20-16)$

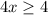
$4x\geq 4$

Divide both sides by 4.

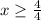
$x\geq (4)/(4)$

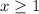
$x\geq 1$

Therefore the solution of given inequality is x ≥1.

Please log in or register to add a comment.