Question

Suppose you have 52 feet of fencing to enclose a rectangular dog pen. The function A = 26x = x2 where x = width, gives you the area of the dog pen in square feet. what width gives you the maximum area? what is the maximum area? round to the nearest tenth if necessary.

Answer 1

Width = 13 ft

Maximum Area = 169 ft²

Explanation:

Given: A rectangular dog pen whose fencing is 52 feet.

Let length be y and width be x

Fencing = 2(l+b)

52 = 2 (x+y)

x + y = 26

y = 26 - x

Area of rectangular pen = Length x width

= y . x

`A=x(26-x)`

`A=26x-x^2`

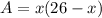
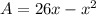
It is parabolic equation. Maximum/Minimum at vertex.

`x=-(b)/(2a)`

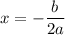
where, a=-1, b=26

`x=(26)/(2)=13`

Now we put x=13 into A

`A=13(26-13)`

`A=169`

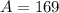
Hence, The width is 13 feet and Maximum area is 169 ft²

Answer 2

maximum area is a square

the side of the square would be 52/4 = 13 feet

area = 13*13 = 169 square feet