A function is odd if f(-x)=-f(x).
So given a function, to check whether it is odd or not, we calculate f(-x). If it is equal to -f(x), then the function is odd; if not, it is not odd.
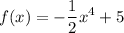
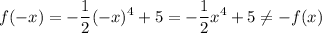
thus the function is not odd
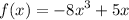

thus the function is odd

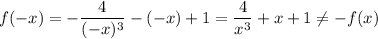
thus the function is not odd
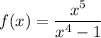
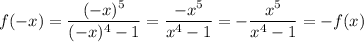
thus the function is odd
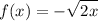
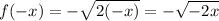
In this particular case f(x) and f(-x) can both exist only for x=0 (because one of them is certainly negative). Thus the function is not odd
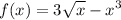
similarly to the previous case, the Domain of f is [0, infinity) and f(-x) cannot be calculated except for x=0. So the function is not odd.