Question

Find the derivative of 4/square root of x

Answer 1

`\displaystyle (dy)/(dx) = \frac{-2}{x^\Big{(3)/(2)}}`

General Formulas and Concepts:

Calculus

Differentiation

• Derivatives
• Derivative Notation

Derivative Property [Multiplied Constant]:
`\displaystyle (d)/(dx) [cf(x)] = c \cdot f'(x)`

Basic Power Rule:

1. f(x) = cxⁿ
2. f’(x) = c·nxⁿ⁻¹

Explanation:

Step 1: Define

Identify

`\displaystyle y = (4)/(√(x))`

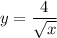
Step 2: Differentiate

1. Derivative Property [Multiplied Constant]:
   `\displaystyle y' = 4 (d)/(dx) \bigg[ (1)/(√(x)) \bigg]`
2. Basic Power Rule:
   `\displaystyle y' = 4 \Bigg( \frac{1}{x^\Big{(3)/(2)}} \Bigg)`
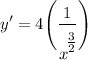
3. Simplify:
   `\displaystyle y' = \frac{4}{x^\Big{(3)/(2)}}`

Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Differentiation