Question

The formula A=P(1+r)t is used to show the total amount owed for a loan with a simple annual interest rate.

Solve for r.

Answer 1

Answer:
`r=((A)/(P))^{(1)/(t)}-1`

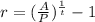
Explanation

Compound interest is the addition of interest to the principal sum of a deposit or a loan.

Let P = principal amount which was taken as a loan then the accumulated amount A is given by

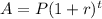`A=P(1+r)^t`.......(1)

where, r is the rate of simple annual interest in decimal.

t is the time applied for interest.

For solving r divide both sides of equation by P in (1),we get

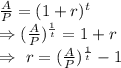`(A)/(P)=(1+r)^t\\\Rightarrow((A)/(P))^{(1)/(t)}=1+r\\\Rightarrow\ r=((A)/(P))^{(1)/(t)}-1`.

Answer 2

We are asked to express r in terms of A, P, and t.

We first divide both sides of the equation by t, which gives us



`\displaystyle{ (A)/(t)=P(1+r)`,


then, dividing both sides by P, we have


`\displaystyle{ (A)/(Pt)=1+r`.

Swap the sides:


`\displaystyle{ 1+r= (A)/(Pt)`

Finally subtracting 1 from both sides gives us


`\displaystyle{ r=(A)/(Pt)-1`.