Answer: The ratio of the volumes of two pyramids is 27 : 1331.
Step-by-step explanation: Given that two two pyramids are similar and the ratio between the length of their edges is 3 : 11.
We are to find the ratio of the volumes of two pyramids.
Let a units and b units be the lengths of the edges of the two pyramids.
The, according to the given information, we have
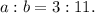
We know that the ratio of the volumes of two similar pyramids is equal to the ratio of the cubes of the lengths of edges of the two pyramids.
Therefore, the ratio of the volumes of two pyramids will be
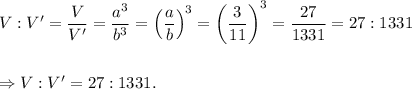
Thus, the ratio of the volumes of two pyramids is 27 : 1331.