Question

A pizza parlor offers a choice of 15 different topping how many for topping pizza are possible

Answer 1

Given:

Number of choices offered, n = 15

Number of toppings (sample), r = 4

Let's find the number of possible 4-topping pizzas possible.

To solve this exercise, we are to use combination.

Combination involves the arrangement of objects without any repitition of orders of arrangement.

Apply the formula:

`^nC_r=(n!)/(r!(n-r)!)`

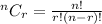
Thus, we have:

`^(15)C_4=(15!)/(4!(15-4)!)`

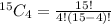
Solving further:

`\begin{gathered} ^(15)C_4=(15!)/(4!(11)!) \\ \\ ^(15)C_4=(15\ast14\ast13\ast12\ast11!)/(4\ast3\ast2\ast1\ast11!) \\ \\ ^(15)C_4=(15\ast14\ast13\ast12)/(4\ast3\ast2\ast1) \\ \\ ^(15)C_4=(32760)/(24) \\ \\ ^(15)C_4=1365 \end{gathered}`

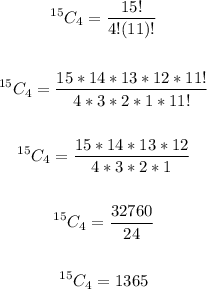
Therefore, there are 1365 possible 4-topping pizzas.

ANSWER:

1365