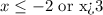Question

Solve the compound inequality 4x - 7 > 5 or 5x+4 3 -6.

Answer 1

The expressions we have are:

`\begin{gathered} 4x-7>5 \\ or \\ 5x+4\leq-6 \end{gathered}`

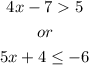
We need to solve each of these expressions, and since it is a compound inequality, the solution will be the solution of the first inequality OR the solution of the second inequality.

We start by solving:

`4x-7>5`

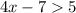
The first step is to add 7 to both sides:

`\begin{gathered} 4x-7+7>5+7 \\ 4x>12 \end{gathered}`

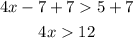
The next step is to divide both sides by 4:

`\begin{gathered} (4x)/(4)>(12)/(4) \\ x>3 \end{gathered}`

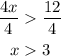
We have the first part of the solution: x>3

Now we need to solve the second inequality:

`5x+4\leq-6`

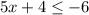
The first step is to subtract 4 to both sides:

`\begin{gathered} 5x+4-4\leq-6-4 \\ 5x\leq-10 \end{gathered}`

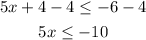
And the second step is to divide both sides by 5:

`\begin{gathered} (5x)/(5)\leq-(10)/(5) \\ x\leq-2 \end{gathered}`

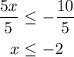
We have the second part of the solution. And since the initial conditions are one inequality OR the other, the same goes to express the solution:

`x\leq-2\text{ or x>}3`

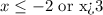
ANSWER: OPTION D

`x\leq-2\text{ or x>}3`