Answer:
a).
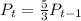
b).
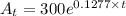
c). 6429 bacteria
Explanation:
Population of the bacteria grows exponentially.
Therefore, growth of the bacteria will be represented by the formula
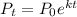
Where
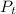 = Population of the bacteria after time t
= Population of the bacteria after time t
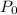 = Initial population of the bacteria
= Initial population of the bacteria
k = growth constant
t = time taken for growth
Now we plug in the values in the formula
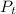 = 500
= 500
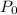 = 300
= 300
Time t = 4 hours
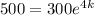
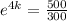
Now we take the natural log (ln) on both the sides
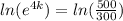
4k(lne) = ln(500) - ln(300)
4k = 6.2146 - 5.7038
4k = 0.5108
k =
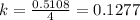
a). Recursive formula for the sequence formed by the bacterial growth
Since
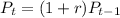
500 = (1 + r)300
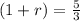
r =
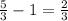
Therefore, the recursive formula will be
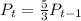
b). Explicit formula for the number of the bacteria will be
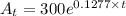
c). We have to calculate the number of bacteria after 24 hours
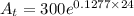
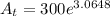
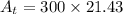
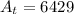 bacteria
bacteria