Question

a cup contains 36 coins, there are twice as many quarters as There are nickels. how many quarters are in the cup.

Answer 1

Given:

Number of coins = 36

There are twice as many quarters as there are nickels.

Let's find the number of quarters in the cup.

Let x represent the number of quarters.

Let y represent the number of nickels.

Since there are twice as many quarters as there are nickels, we have:

x = 2y

In this situation, we have the system of equations:

• x + y = 36

,

• x = 2y

Let's solve the system of equation simltaneously using substitution method.

Substitute 2y for x in equation 1:

2y + y = 36

3y = 36

Divide both sides by 3:

`\begin{gathered} (3y)/(3)=(36)/(3) \\ \\ y=12 \end{gathered}`

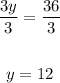
Substitute 12 for y in either equation.

Take equation 2:

x = 2y

x = 12(2)

x = 24

We have the solution:

x = 24, y = 12

Therefore, there are 24 quarters and 12 nickels in the cup.

ANSWER:

There are 24 quarters in the cup.