first we need the values multiplying by 4
so we order the values from lowest to highest and multiply
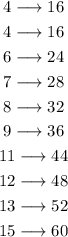
the mean is the average, so sum all the number and divide by the quantity
the total sum is 356 and must divide by 10(the number of values)
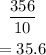
the mean is 35.6
the median is the average between the 2 centrak numbers on this case 32 and 36
so
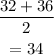
the median is 34
the mode is the value that is repeated the most within all
we can notice that 16 is twice and the other values only once
so the mode is 16
The range is the substrac from the larger number and the smaller number
so
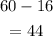
then the range is 44
The standard deviation must calcuate with this equation
_(\square)](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/eghnfaexi0v87iyqpmlu.png)
the symbol that looks like a 3 on the contrary means "the sum of", X is a value, u is the mean and N the total of numbers
so, first we need to calculate the sum
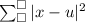
replacing x for each number and finding the solution
to 16
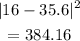
to 24
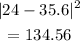
to 28
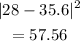
to 32

to 36
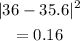
to 44
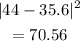
to 48
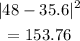
to 52
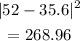
to 60
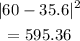
now, we add everything
and the result is
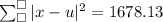
and replace all on the equation
![\begin{gathered} \sqrt[]{(1678.13)/(10)} \\ \\ =12.95 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/axphzph38p2sgv0fdy4r.png)
the standard deviation is 12.95