For this problem, we are given a certain a data set and we need to find the number of data within 1 population standard deviation of the mean.
The data set is:
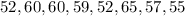
The first step we need to take is to reorder the data set.
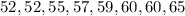
Now we need to determine the mean:

Finally, we have to find the standard deviation:
![\begin{gathered} \sigma=\sqrt{((52-57.5)^2+(52-57.5)^2+(55-57.5)^2+(57-57.5)^2+(59-57.5)^2+(60-57.5)^2+(60-57.5)^2+(65-57.5)^2)/(8)}\\ \\ \sigma=\sqrt{(138)/(8)}=√(17.25)=4.15 \end{gathered}]()
Now we need to find the range within 1 standard deviation from the mean:
![\begin{gathered} [57.5-4.15,57.5+4.15\rbrack\\ \\ \lbrack53.35,61.65\rbrack \end{gathered}]()
The range of values within one standard deviation goes from 53.35 to 61.65. Therefore there are a total of 5 values within this range.