Question

What would be the maximum value for f(x) = −5x2 + 9

Answer 1

well, looking at the expression, it has a -5 on the leading term, that means is not just a quadratic, but is a parabolic graph and because the coefficient of the leading term is negative, is upside-down, or opening downwards.

because it opens downwards, it looks like an arc, comes from the bottom up up up gets to a "maximum" or U-turn (vertex), then goes back down down down. So, where's the vertex anyway?


`\bf \textit{ vertex of a vertical parabola, using coefficients}\\\\ \begin{array}{lccclll} f(x) = &{{ -5}}x^2&{{ +0}}x&{{ +9}}\\ &\uparrow &\uparrow &\uparrow \\ &a&b&c \end{array}\qquad \left(-\cfrac{{{ b}}}{2{{ a}}}\quad ,\quad {{ c}}-\cfrac{{{ b}}^2}{4{{ a}}}\right) \\\\\\ \left( -\cfrac{0}{2(-5)}~~,~~9-\cfrac{0}{4(-5)} \right)\implies (0~~,~~9)`

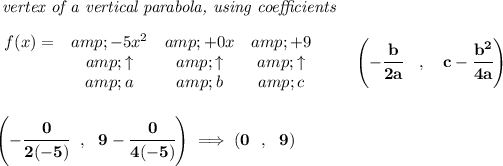
so, that's where the vertex is, and the maximum value for f(x), is the y-coordinate of course, or 9.