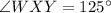Question

In

kite WXYZ, m∠ZWY=43°and m∠XYW=12°.
 
What is m∠WXY?


Enter your answer in the box.



photo:

Answer 1

Answer:
`\angle WXY=125^(\circ)`

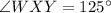
Step-by-step explanation: Since, a kite has one pair of congruent angles and its main diagonal bisects its opposite angles.

Therefore, According to the given figure,

`\angle WXY=\angle WZY`

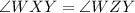
And, WY is the main diagonal which bisects angles ZWX and XYZ.

So,
`\angle ZWX =2* \angle ZWY= 2* 43^(\circ)=86^(\circ)`

And,
`\angle XYZ =2* \angle XYW= 2* 12^(\circ)=24^(\circ)`

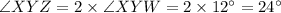
Since, Sum of all angles of a quadrilateral is equal to
`360^(\circ)`

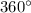
Therefore,
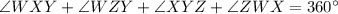
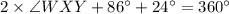
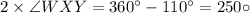
`\angle WXY+\angle WZY+\angle XYZ+\angle ZWX=360^(\circ)`

⇒
`2* \angle WXY+ 86^(\circ)+24^(\circ)=360^(\circ)`

⇒
`2* \angle WXY=360^(\circ)-110^(\circ)=250{\circ}`

⇒
`\angle WXY=125^(\circ)`