Question

Can we obtain a diagonal matrix by multiplying two non-diagonal matrices? give an example

Answer 1

Yes, we can obtain a diagonal matrix by multiplying two non-diagonal matrices. A diagonal matrix is a matrix where all the elements beyond the diagonal are zeros. This is an example.

`\left[\begin{array}{ccc}1&3&4\\0&-8&-9\\0&0&- (55)/(8) \end{array}\right] \cdot \left[\begin{array}{ccc}1&-3&- (5)/(8) \\0&1&- (9)/(8) \\0&0&1\end{array}\right] = \left[\begin{array}{ccc}1&0&0\\0&-8&0\\0&0&- (55)/(8) \end{array}\right]`

Answer 2

Yes, we can obtain a diagonal matrix by multiplying two non diagonal matrix.

Consider the matrix multiplication below


`\left[\begin{array}{cc}a&b\\c&d\end{array}\right] \left[\begin{array}{cc}e&f\\g&h\end{array}\right] = \left[\begin{array}{cc}a e+b g&a f+b h\\c e+d g&c f+d h\end{array}\right]`

For the product to be a diagonal matrix,

a f + b h = 0 ⇒ a f = -b h
and c e + d g = 0 ⇒ c e = -d g

Consider the following sets of values


`a=1, \ \ b=2, \ \ c=3, \ \ d = 4, \ \ e=(1)/(3), \ \ f=-1, \ \ g=-(1)/(4), \ \ h=(1)/(2)`

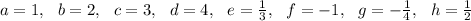
The the matrix product becomes:


`\left[\begin{array}{cc}1&2\\3&4\end{array}\right] \left[\begin{array}{cc}(1)/(3)&-1\\-(1)/(4)&(1)/(2)\end{array}\right] = \left[\begin{array}{cc}(1)/(3)-(1)/(2)&-1+1\\1-1&-3+2\end{array}\right]= \left[\begin{array}{cc}-(1)/(6)&0\\0&-1\end{array}\right]`

Thus, as can be seen we can obtain a diagonal matrix that is a product of non diagonal matrices.