Question

The saginaw bay tides vary between 2 feet and 8 feet. the tide is at its lowest point when time (t) is 0 and completes a full cycle in 16 hours. what is the amplitude, period, and midline of a function that would model this periodic phenomenon? amplitude = 3 feet; period = 16 hours; midline: y = 5 amplitude = 3 feet; period = 8 hours; midline: y = 3 amplitude = 6 feet; period = 16 hours; midline: y = 5 amplitude = 6 feet; period = 8 hours; midline: y = 3

Answer 1

A] amplitude = 3 feet; period = 16 hours; midline: y = 5

Hope this helps (:

Answer 2

Option A

amplitude = 3 feet; period = 16 hours; midline: y = 5 amplitude = 3 feet;

Explanation:

Given that The saginaw bay tides vary between 2 feet and 8 feet.

When we correspond these to sine curve we can say minimum 2 ft max 8 ft middle value being 5 ft

Period = 16 hours (since it completes one full cycle in 16 hours_

Amplitude = maximum - middle value or middle value-minimum

=
`8-5 = 5-2 = 3 ft`

Thus the equation would be as
`y = 3sin (8)/(\pi)+5`

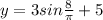
Thus we find that minimum =2, max =8 middle line y=5

Amplitude = 3 ft and period = 16

Hence option A is right.