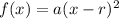Question

Which second-degree polynomial function has a leading coefficient of –1 and root 5 with multiplicity 2?

Answer 1

f(x) = 2x2 – 4x – 30

Explanation:

Got it right

Answer 2

A second degree polynomial function has the general form:


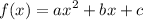
`\displaystyle{f(x)=ax^2+bx+c`, where
`a\\eq0`.

The leading coefficient is a, so we have a=-1.

5 is a double root means that :

i) f(5)=0,
ii) the discriminant D is 0, where
`D=b^2-4ac`.

Substituting x=5, we have

f(5)=a(5)^2+b(5)+c,

and since f(5)=0, and a is -1 we have:

0=-25+5b+c
thus c=25-5b.


By ii)
`\displaystyle{b^2-4ac=0`.

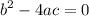
Substituting a with -1 and c with 25-5b we have:


`\displaystyle{b^2-4ac=0`

`\displaystyle{b^2-4(-1)(25-5b)=0`

`\displaystyle{b^2+4(25-5b)=0`

`\displaystyle{b^2-20b+100=0`

`\displaystyle{(b-10)^2=0`

`\displaystyle{b=10`


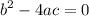
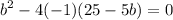
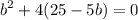
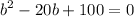
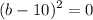
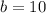
Finally we find c: c=25-5b=25-50=-25

Thus the function is
`\displaystyle{f(x)=-x^2+10x-25`


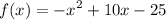
Remark: It is also possible to solve the problem by considering the form


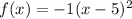
`f(x)=-1(x-5)^2` directly.

In general, if a quadratic function has leading coefficient a, and has a root r of multiplicity 2, then its form is
`f(x)=a(x-r)^2`