Question

find the slope of the line passing through each pair of points or state that the slope is undefined. Then indicate whether the line through the points rises, falls, is horizontal, or is vertical.Its for (-3, 3/4) and (6, 1/4)

Answer 1

We have the following points:

`\begin{gathered} (x_1,y_1)=(-3,(3)/(4)) \\ (x_2,y_2)=(6,(1)/(4)) \end{gathered}`

The slope (m) of two given points is given by

`m=(y_2-y_1)/(x_2-x_1)`

By substituting our coordinate points into the slope formula, we have

`m=((1)/(4)-(3)/(4))/(6-(-3))`

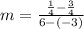
which gives

`\begin{gathered} m=(-(2)/(4))/(6+3) \\ or\text{ equivalently,} \\ m=(-(1)/(2))/(9) \end{gathered}`

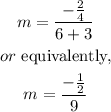
By simplying this result, the slope is equal to:

`m=-(1)/(18)`

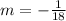
From this result, we can see that the slope is negative, which means that the line through the points falls to the right as we can see on the following picture: