Answer:
Both the equation and its inverse are functions.
Explanation:
A function is relation in which one input gives one and only one output.
Here, the given function,
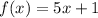
Which is a polynomial,
A polynomial is a function because for each input value it gives only one output value.
⇒ f(x) is a function.
Now, For finding the inverse of f(x),
Replace f(x) by y,
y = 5x + 1
Switch x and y,
x = 5y + 1
Isolate y on the left side,
-5y = 1 - x
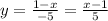
Replace y by
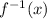 ,
,
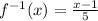
Which is also a polynomial,
Hence, the inverse of f(x) is also a function,
Last option is correct.