Question

Which of the following is true for the relation f(x) = 2x2 + 1?

Only the equation is a function.


Neither the equation nor its inverse is a function.


Both the equation and its inverse are functions.


Only the inverse is a function.

Answer 1

Neither the equation nor its inverse is a function

Answer 2

Both the equation and its inverse are functions.

Explanation:

Since, a relation is called a function when an input value of the relation has only one output value,

Here, the given relation,

`f(x) = 2x^2 + 1`

When we plot the graph of this function,

We observed that all vertical line intersects the graph exactly once, except

, x = 0,

Thus, by vertical line test,

In the given equation every x has only one output value,

⇒ f(x) is a function,

Now, the inverse of a function is also a function,

⇒
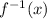`f^(-1)(x)` is also a function,

Hence, Both the equation and its inverse are functions.