Question

angle efg and angle gfh are a linear pair, the measure of angle efg equals 4n+20, and measure of angle gfh equals 3n+13. what are the measures of angle efg and angle gfh?

Answer 1

A linear pair of angles are defined to equal 180 degrees. This means that you can add both expressions together and set them equal to 180 degrees. Once, you've done this, isolate the variable n in the equation and plug in the value to determine each angle.

Answer 2

∠EFG=104° and ∠GFH=76°

Explanation:

Given information:∠EFG = (4n+20)°, ∠GFH = (3n+13)° and ∠EFG and ∠GFH are a linear pair.

If two angles are a linear pair, then the sum of those angles is 180°.

It is given that ∠EFG and ∠GFH are a linear pair.

`\angle EFG+\angle GFH=180^(\circ)`

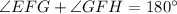
Substitute the given values.

`(4n+20)+(3n+13)=180`

Combined like terms.

`(4n+3n)+(20+13)=180`

`7n+33=180`

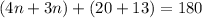
Subtract 33 from both sides.

`7n+33-33=180-33`

`7n=147`

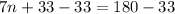
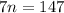
Divide both sides by 7.

`n=21`

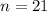
The value of n is 21.

`\angle EFG=4n+20=4(21)+20=104^(\circ)`

`\angle GFH=3n+13=3(21)+13=76^(\circ)`

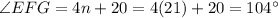
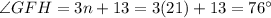
Therefore, the measure of ∠EFG and ∠GFH are 104° and 76° respectively.