Question

You decide to put $100 in a savings account to save for a $3,000 down payment on a new car. If the account has an interest rate of 2% per year and is compounded monthly, how long does it take you to earn $3,000 without depositing any additional funds?

Answer 1

when you plug into equation A=P(1+r/n)^nt, t=170

Answer 2

170.202 years

Explanation:

From the compound interest formula, that has interest rate in times per year but compounds monthly we have

`A=P(1+(r)/(n))^(nt)`

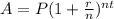
A is the amount you want to save, P is the principal (what you put down, in this case 100), r is the anual interest rate, n is 12 i.e the times it compounds, and t is the amount of years it will take. So we have data for all variables but t.

Solving for t we have

`(A)/(P)=(1+(r)/(n))^(nt)`

taking logs

`log((A)/(P))=nt \,log(1+(r)/(n))`

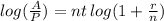
finally

`t = \frac {log((A)/(P)) }{ n[log(1 + (r)/(n))]}`

replacing and calculating we get t=170.202