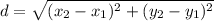Question

Find the distance between 0,3 and -2-5 round nearest hundreth

Answer 1

I want to draw your attention to the connection finding the distance between two points has with one of the oldest and most ubiquitous theorems in mathematics: the Pythagorean Theorem. If you'll recall, the Pythagorean Theorem states that, in any right triangle, the sum of the squares of its legs is equal to the square of its hypotenuse (the side opposite the triangle's right angle), or more formally:

a²+b²=c², where a and b are the length of the legs of the triangle, and c is the length of its hypotenuse.

What does that have to do with finding the distance between two points? For that, I want you to take a look at the two images I've attached to this post. If we just plot the two points on the x-y plane and draw a line between them, the connection to Pythagoras isn't too obvious, but when we connect the x and y components of the points, it should become immediately clear. The vertical and horizontal components of the points combine with the diagonal to form a right triangle, and the distance is the length of its hypotenuse!

We can't apply the theorem yet, though; we'll first need to find the lengths of the legs before we can determine the length of the hypotenuse. For that, we'll need to find the distance between each of the points' corresponding coordinates. To find those, we just need to subtract those coordinates from one another. We find the distance between the x coordinates to be 0 - (-2) = 2 and the distance between the y coordinates to be 3 - (-5) = 8.

(Note that we could've chosen to do the subtraction the other way around, too, obtaining negative differences. Usually, we'd deal with these by taking the absolute value of the result, but in this case, our answers will get squared away - literally - by the Pythagorean Theorem.)

Now that we have the legs of the triangle, we're ready to find the hypotenuse. We enter our values in:

2²+8² = d²
4 + 64 = d²
68 = d²
√68 = d

(we've chosen d here to represent "distance," though it plays the same role c did in the other statement of the theorem)

And from there, you can use the calculator of your choosing to get a good approximation.

One last note: here's a generalization of everything we did here, now that you have some background for why it is the way it is, and where exactly it comes from:

For any two points
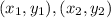`(x_1,y_1), (x_2,y_2)`:


`d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2`

Answer 2

The answer is 8.25
The formula for distance will be the √ (x2-x1)²+(y2-y1)². (as you can see)
Don't be intimidated!
Step one:
Take the two cordinates (0,3) and (-2,-5)
Step two: It doesn't matter which one you choose, but choose one to be your x1,y1 and another to be your x2,y2
In this situation I choose (0,3) to represent (x1,y1) and (-2,-5) to represent (x2,y2). DO NOT over think this, you got it!
Final Step:
Simply plug those numbers into the represented formula it should end up like
√(-2-0)²+(-5-3)²
Simply solve it yourself or use a calculator such as Desmos to find you answer

Hope this helps!