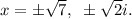Question

What are the solutions of the equation x4 – 5x2 – 14 = 0? Use factoring to solve.

Answer 1

(x2 - ) (x2 + ) = 0
(x2 - 7) (x2 + 2) = 0
(x2 - 7) = 0 and (x2 + 2) = 0
x2 = 7 and x2 = - 2
√x2 = √7 and √x2 = √-2
x = √7 and x = √-2 --> it doesn't exist

Answer 2

Answer: The required solutions of the given equation are

`x=\pm\sqrt7,~\pm\sqrt2i.`

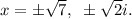
Step-by-step explanation: We are given to find the solutions of the following bi-quadratic equation :

`x^4-5x^2-14=0~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

Let us consider that

`x^2=y~~~~~\Rightarrow x^4=y^2.`

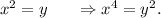
So, equation (i) becomes

`y^2-5y-14=0,`

which is a quadratic equation in the variable y. The above equation in variable y can be solved using factorization as follows :

`y^2-5y-14=0\\\\\Rightarrow y^2-7y+2y-14=0\\\\\Rightarrow y(y-7)+2(y-7)=0\\\\\Rightarrow (y-7)(y+2)=0\\\\\Rightarrow y-7=0,~~~y+2=0\\\\\Rightarrow y=7,-2.`

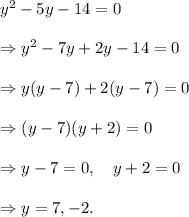
Therefore, we get

`x^2=7\\\\\Rightarrow x=\pm\sqrt7`

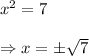
and

`x^2=-2\\\\\Rightarrow x=\pm√(-2)\\\\\Rightarrow x=\pm\sqrt2i,~~~~~~~~~~~~~[\textup{where }i=√(-1)]`

Thus, the required solutions of the given equation are

`x=\pm\sqrt7,~\pm\sqrt2i.`