Question

Solve for n.

3(n+6)≥3n+8


no solution
all real numbers
n≥7
n≥23

Answer 1

3(n+6) ≥ 3n+8

Start by distributing....

3n + 18 ≥ 3n + 8

Subtract 3n from both sides to get the n's on the same side....

18 ≥ 8

There are no solutions because 18 is not less than or equal to 8

Answer 2

The correct option is B) all real numbers.

Explanation:

Consider the provided inequity.

`3(n+6)\geq 3n+8`

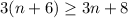
We need to solve the inequity for n.

`3(n+6)\geq 3n+8`

`3n+18\geq 3n+8`

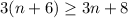
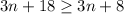
Subtract 3n from both sides

`3n-3n+18\geq 3n-3n+8`

`18\geq 8`

Which is true for any real number. As 18 is greater than 8.

Hence, the value of n is all real numbers.

Thus the correct option is B) all real numbers.