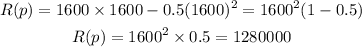Question

A boat manufacturer found that the revenue from sales of a ski-boat is a function of the unit price p that it charges. If the revenue is R(p) = 1600p - 0.5p2, what unit price p should the company charge in order to maximize revenue? What is the maximum revenue?

Answer 1

the given relation is

`\begin{gathered} R(p)=1600p-0.5p2 \\ R(p)=-0.5p^2+1600p \end{gathered}`

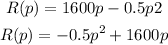
compare the above expression with the standard parabola quadratic equation

`ax^2+bx+c=0`

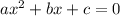
so the value of a = -0.5

b = 1600

c = 0

the maximum value will be on

`p=-(b)/(2a)`
`\begin{gathered} p=(-1600)/(2*-0.5)=(16000)/(10) \\ =1600 \\ \end{gathered}`

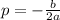
a) so the unit price of the boat should be p = 1600.

and the maximum revenue will be

put p = 1600

`\begin{gathered} R(p)=1600*1600-0.5(1600)^2=1600^2(1-0.5) \\ R(p)=1600^2*0.5=1280000 \\ \\ \end{gathered}`