Question

3.Write the equation of a parabola with focus (-2, 4) and directrix y = 2. Show your work, including a sketch.

Answer 1

In this problem, we need to find the equation and the graph of a parabola given the focus and the directrix.

Sometimes it's best to start with graphing the given information to determine if the graph is a horizontal or vertical parabola. So, we'll have:

Since the focus is always inside the parabola and the directrix is outside the parabola, we know this will be a vertical parabola. Depending on the text, this standard formula may look different. For our purposes, the standard form of a vertical parabola is:

`(x-h)^2=4p(y-k)`

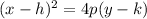
Where (h,k) is the vertex.

The vertex is typically the same distance from both the focus and the directrix, so we can find the distance between them and divide by 2.

The vertex will be at (-2,3):

Now we can substitute the vertex into our standard form knowing (h,k) = (-2, 3):

`\begin{gathered} (x-(-2))^2=4p(y-3) \\ (x+2)^2=4p(y-3) \end{gathered}`

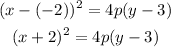
Next, we need to find the value of p for our equation.

P is the distance from the vertex to the focus. Since our vertex is at (-2,3) and our focus is at (-2,4), the difference between the y-values shows a distance of 1.

Since p=1,

`\begin{gathered} (x+2)^2=4(1)(y-3) \\ (x+2)^2=4(y-3) \end{gathered}`

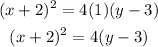
Our final graph is: