Part A:
Given
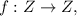
defined by
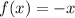
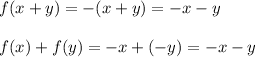
but
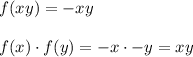
Since, f(xy) ≠ f(x)f(y)
Therefore, the function is not a homomorphism.
Part B:
Given
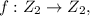
defined by
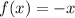
Note that in
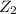
, -1 = 1 and f(0) = 0 and f(1) = -1 = 1, so we can also use the formular
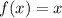
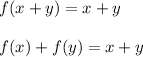
and
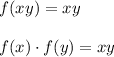
Therefore, the function is a homomorphism.
Part C:
Given
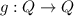
, defined by
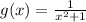
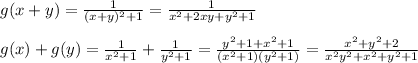
Since, f(x+y) ≠ f(x) + f(y), therefore, the function is not a homomorphism.
Part D:
Given
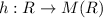
, defined by
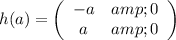
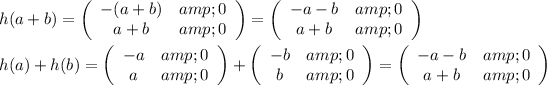
but
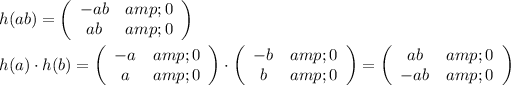
Since, h(ab) ≠ h(a)h(b), therefore, the funtion is not a homomorphism.
Part E:
Given
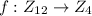
, defined by
![\left([x_(12)]\right)=[x_4]](https://img.qammunity.org/2018/formulas/mathematics/college/310f3a4q2qi5szkzkrw24uu6dtiqxooblo.png)
, where
![[u_n]](https://img.qammunity.org/2018/formulas/mathematics/college/mb2jjss6xv8k2awfmyjj5ep3d6iq9ogj1p.png)
denotes the lass of the integer

in
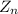
.
Then, for any
![[a_(12)],[b_(12)]\in Z_(12)](https://img.qammunity.org/2018/formulas/mathematics/college/f2hpfhwifxtfsypfipyrd0ar861a7gvvb0.png)
, we have
![f\left([a_(12)]+[b_(12)]\right)=f\left([a+b]_(12)\right) \\ \\ =[a+b]_4=[a]_4+[b]_4=f\left([a]_(12)\right)+f\left([b]_(12)\right)](https://img.qammunity.org/2018/formulas/mathematics/college/oyfcgkvm9q851bjfi256kpe1lglr3svydc.png)
and
![f\left([a_(12)][b_(12)]\right)=f\left([ab]_(12)\right) \\ \\ =[ab]_4=[a]_4[b]_4=f\left([a]_(12)\right)f\left([b]_(12)\right)](https://img.qammunity.org/2018/formulas/mathematics/college/3a5i4sxpzpf0m5lul35kak2ck5ylk2xxgx.png)
Therefore, the function is a homomorphism.