Answer:
![\frac{5\sqrt[3]{6}}{8}](https://img.qammunity.org/2018/formulas/mathematics/high-school/vq8dc99fi1s202e3nsdz3d4pm118nqk0x3.png)
Explanation:
We have been given an exponential number. We are supposed to simplify our given number.
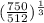
Using fractional exponent rule
![x^(m)/(n)=\sqrt[n]{x^m}](https://img.qammunity.org/2018/formulas/mathematics/high-school/8opzeh3rhsnors849ee7rf7y3wzmkp6e24.png) , w ecan write our given number as:
, w ecan write our given number as:
![((750)/(512))^{(1)/(3)}=\sqrt[3]{((750)/(512))^1}](https://img.qammunity.org/2018/formulas/mathematics/high-school/unx7c2sk58t97q1w76veilpesxy1zxrlxj.png)
![((750)/(512))^{(1)/(3)}=\sqrt[3]{(750)/(512)}](https://img.qammunity.org/2018/formulas/mathematics/high-school/j084pojesouubfwvk2nouffsw0vzji4p2y.png)
We can rewrite 512 as
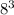 and 750 as 125*6.
and 750 as 125*6.
![((750)/(512))^{(1)/(3)}=\sqrt[3]{(125*6)/(8^3)}](https://img.qammunity.org/2018/formulas/mathematics/high-school/r0lf8mtzinzkou02k6f5bz9zyuqxfduc5j.png)
We can rewrite 125 as
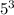
![((750)/(512))^{(1)/(3)}=\sqrt[3]{(5^3*6)/(8^3)}](https://img.qammunity.org/2018/formulas/mathematics/high-school/cq5afhns4j8p4s2tmb5xrlzk7l6951bvn3.png)
Using radical rule
![\sqrt[n]{a^n}=a](https://img.qammunity.org/2018/formulas/mathematics/middle-school/rhnmh96n3lj3vyi740p9ih043v5wwzushn.png) , we will get:
, we will get:
![((750)/(512))^{(1)/(3)}=\frac{5\sqrt[3]{6}}{8}](https://img.qammunity.org/2018/formulas/mathematics/high-school/5au828zvkvxfk30e1hc1j25khxsnn9sgvn.png)
Therefore,
![\frac{5\sqrt[3]{6}}{8}](https://img.qammunity.org/2018/formulas/mathematics/high-school/vq8dc99fi1s202e3nsdz3d4pm118nqk0x3.png) is equivalent to our given number.
is equivalent to our given number.