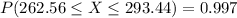Question

Fuel economy estimates for automobiles built in a certain year predicted a mean of 278 mpg and a standard deviation of 5.2 mpg for highway driving. Assume that anormal distribution can be applied. Within what range are 99.7% of the automobiles?

Answer 1

The distribution of the fuel consumption can be considered to have a normal distribution with mean μ=278 mpg and standard deviation σ= 5.2 mpg.

You have to determine within what range of fuel consumption you find 99.7% of the automobiles of the market.

First, let's draw a sketch under the normal distribution to visualize the lower and upper limits of the range to determine:

In the normal curve, the green shaded area between the values I named x₁ and x₂ represents 99.7% of the distribution. The remaining 0.3% is in the little tails found below x₁ and above x₂.

You can express this shaded area as a probability, where X represents the variable of interest:

`P(x_1\leq X\leq x_2)=0.997`

To determine this interval, you have to determine the difference between the accumulated probability up to x₂ and the accumulated probability up to x₁, so that:

`P(X\leq x_2)-P(X\leq x_1)=0.997`

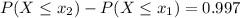
The probability accumulated until the lowest limit of the interval, x₁, is represented by the left tail shown in the image, so that:

`P(X\leq x_1)=0.0015`

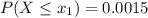
And the probability accumulated until the highest limit of the interval, x₂, is equal to the area under the curve until that value, that is the sum of 0.0015 and 0.997:

`\begin{gathered} P(X\leq x_2)=0.0015+0.997 \\ P(X\leq x_2)=0.9985 \end{gathered}`

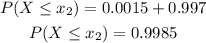
Knowing the accumulated probabilities for both limits of the interval, you can use the standard normal distribution to determine them.

The standard normal distribution is defined as follows:

`Z=(X-\mu)/(\sigma)N(0,1)`

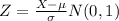
Under the standard normal distribution, both values will accumulate the same probability, using these values of probability you can determine the z values and then reverse the standardization to "translate" the said Z-values to values of the variable:

Value of x₁

Under the standard normal distribution:

`P(Z\leq z_1)=0.0015`

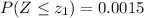
The value under the standard normal distribution that has an accumulated probability of 0.0015 is z₁=-2.97

Using the formula of the standard normal distribution we can translate this value to a value of the variable:

`z_1=(x_1-\mu)/(\sigma)`

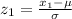
Write the expression for x₁:

`\begin{gathered} z_1\cdot\sigma=x_1-\mu \\ x_1=(z_1\cdot\sigma)+\mu \end{gathered}`

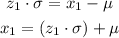
For μ=278 and σ= 5.2 mpg:

`\begin{gathered} x_1=(-2.97\cdot5.2)+278 \\ x_1=-15.4444+278 \\ x_1=262.556 \end{gathered}`

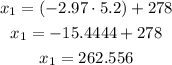
The lower value of the interval is x₁=262.56 mpg

Value of x₂

Under the standard normal distribution, this value also accumulates the same probability as under the normal distribution, so that:

`P(Z\leq z_2)=0.9985`

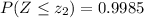
Using the distribution entry, you can determine the corresponding Z-value.

The value under the standard normal distribution that accumulates 0.9985 of probability is z₂= 2.97

Use the standard normal distribution to determine the value of x₂:

`\begin{gathered} z_2=(x_2-\mu)/(\sigma) \\ _{} \end{gathered}`

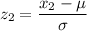
Write the expression for x₂

`\begin{gathered} z_2\cdot\sigma=x_2-\mu \\ x_2=(z_2\cdot\sigma)+\mu \end{gathered}`

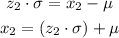
For μ=278 and σ= 5.2 mpg:

`\begin{gathered} x_2=(2.97\cdot5.2)+278 \\ x_(2)=15.444+278 \\ x_(2)=293.444 \end{gathered}`

The upper value of the interval is x₂=293.44 mpg

99.7% of the automobiles are expected to be between the fuel consumption values of 262.56mpg and 293.44 mpg, you can express this symbolically as:

`P(262.56\leq X\leq293.44)=0.997`