Question

Line segment JL is an altitude in triangle JKM. Which statement explains whether JKM is a right triangle? Round measures to the nearest tenth.

A) JKM is a right triangle because KM = 15.3.
B) JKM is a right triangle because KM = 18.2.
C) JKM is not a right triangle because KM ≠ 15.3.
D) JKM is not a right triangle because KM ≠ 18.2.

Answer 1

I just took the test it is C

Answer 2

C. JKM is not a right triangle because KM ≠ 15.3.

Explanation:

We can see from our diagram that triangle JKM is divided into right triangles JLM and JLK.

In order to triangle JKM be a right triangle
`KM^(2)=JK^(2)+JM^(2)`.

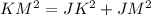We will find length of side KM using our right triangles JLM and JLK as
`KM=KL+LM`.

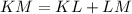Using Pythagorean theorem in triangle JLM we will get,

`LM=\sqrt{JM^(2)-JL^(2)}`

`LM=\sqrt{8^(2)-5^(2)}`

`LM=√(64-25)`

`LM=√(39)=6.244997998\approx 6.24`

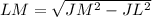
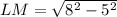
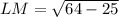
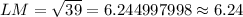
Now let us find length of side KL.

`KL=\sqrt{JK^(2)-JL^(2)}`

`KL=\sqrt{13^(2)-5^(2)}`

`KL=√(169-25)`

`KL=√(144)=12`

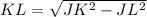
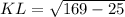
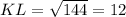
Now let us find length of KM by adding lengths of KL and LM.

`KM=12+6.24=18.24`

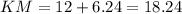
Now let us find whether JKM is right triangle or not using Pythagorean theorem.

`KM^(2)=JK^(2)+JM^(2)`

`18.24^(2)=13^(2)+8^(2)`

`18.24^(2)=169+64`

`18.24^(2)=233`

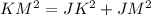
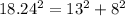
Upon taking square root of both sides of equation we will get,

`18.24\\eq 15.264337522473748`

`18.2\\eq 15.3`

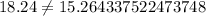
We have seen that KM equals 18.2 and in order to JKM be a right triangle KM must be equal to 15.3, therefore, JKM is not a right triangle and option C is the correct choice.