Question

Two airplanes left the same airport and arrived at the same destination at the same time. The first airplane left at 8:00 a.m. and traveled at an average rate of 496 miles per hour. The second airplane left at 8:30 a.m. and traveled at an average rate of 558 miles per hour. Let x represent the number of hours that the first plane traveled. How many hours did it take the first plane to travel to the destination? Enter an equation that can be used to solve this problem

Answer 1

If d is the distance involved
then for first plane d = 496x

and for second plane its d = 558/(x - 0.5) , so:-

496x = 558x - 279

62x = 279

x = 4.5 hours

The first plane took 4 and a half hours

Answer 2

4.5 hours

`496 x= 558 x-279`

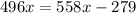
Explanation:

We are given that two airplanes left the same airport and arrives at the same destination at the same time.

We have to find the number of hours taken by first plane to travel to the destination and find the equation that can be used to solve this problem

We are given that the first airplane left at 8:00 a.m

Let y be the distance traveled by the first airplane

The average rate of first airplane =496 miles per hour

The average rate of second airplane =558 miles per hour

Let x represents the number of hours that the first airplane traveled.

The number of hours that the second plane traveled =x-0.5

Because the second airplane take half an hour less than the first airplane

We know that
`distance=speed* time`

`d=496 x`

`d=558(x-0.5)`

`496 x= 558 x-279`

`279=558 x-496 x`

`279=62 x`

`x=(279)/(62)`

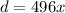
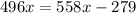
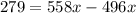
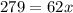
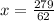
x=4.5 hours

Hence, the first airplane takes 4.5 hours to travel to the destination.