Question

G use lagrange multipliers to find the volume of the largest rectangular box in the first octant with three faces in the coordinate planes and one vertex in the given plane.x + 9y + 8z = 27

Answer 1

This basically comes down to maximizing
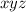
`xyz` subject to
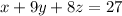
`x+9y+8z=27` and enforcing
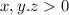
`x,y.z>0`. We have the Lagrangian


`L(x,y,z,\lambda)=xyz+\lambda(x+9y+8z-27)`

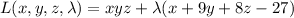
with partial derivatives (set equal to 0 to find critical points)


`\begin{cases}L_x=yz+\lambda=0\\L_y=xz+9\lambda=0\\L_z=xy+8\lambda=0\\L_\lambda=x+9y+8z-27=0\end{cases}`

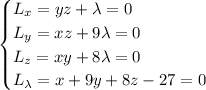
Solving the first equation for
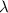
`\lambda` gives
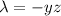
`\lambda=-yz`. Substituting this into the next two equations, we have


`xz-9yz=0\implies z(x-9y)=0\implies x=9y`

`xy-8yz=0\implies y(x-8z)=0\implies x=8z`

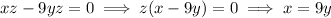
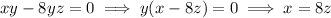
Now


`x+9y+8z=27\implies x+x+x=3x=27\implies x=9`

`x=9y\implies y=1`

`x=8z\implies z=\frac98`

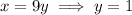
So the vertex of the cuboid in the given plane that maximizes the cuboids volume is
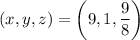
`(x,y,z)=\left(9,1,\frac98\right)`, giving a volume of
`\frac{81}8`.