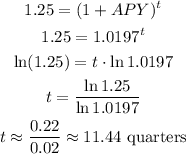The initial deposit is $1500, the annual rate is 1.96%, compounded quarterly.
For a given annual rate r and n compounded periods, the APY is given by:
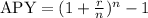
a) For r = 0.0196 and n = 4, we have:
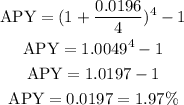
b) $2000 represent an increase of 25% in relation to $1500. In this case, we have: