Question

The vertex form of the equation of a parabola is x=8(y-1)^2-15. What is the standard form of the equation?

Answer 1

x = 8(y-1)^2 - 15

Standard form looks like this, x^2 -6x + 8, or y^2 - 6y + 8
To convert your equation into standard form all we have to do is expand it fully:
x = 8(y-1)^2 - 15
x = 8(y-1)(y-1) - 15
x = 8(y^2 -2y + 1) - 15
x = 8y^2 -16y + 8 - 15
x = 8y^2 -16y - 7

Answer 2

The standard form of the equation is:

`x=8y^2-16y-7`

Explanation:

We know that the standard form of a quadratic equation is given by the expression:

`x=ay^2+by+c`

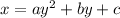
where a,b and c are real numbers.

and a≠0

Here we are given the vertex form of the equation of a parabola by:

`x=8(y-1)^2-15`

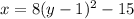
Now, on expanding the parentheses term by using the formula:

`(a-b)^2=a^2+b^2-2ab`

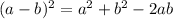
Here a=y and b= 1

Hence, we have:

`x=8(y^2+1-2y)-15\\\\i.e.\\\\x=8* y^2+8* 1-2y* 8-15\\\\i.e.\\\\x=8y^2+8-16y-15\\\\i.e.\\\\x=8y^2-16y+8-15`

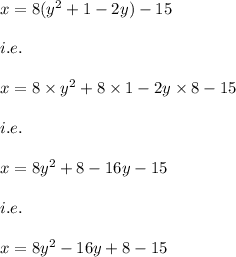
( Since, in the last step we combined the constant term i.e. 8 and -15 )

Hence, we get the standard form of the equation as:

`x=8y^2-16y-7`