Question

The speedometer in Erin’s car is accurate within 2 miles per hour. It currently reads

56 mph. Write and solve an absolute value inequality to represent the situation. At what speeds could Erin be driving?

Answer 1

Answers:

• The absolute value inequality is
  `|\text{x}-56| \le 2`
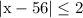
• which solves to
  `54 \le \text{x} \le 58\\\\`
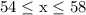
• Her true speed could be anything between 54 mph and 58 mph, including both endpoints.

===================================================

Step-by-step explanation:

x = Erin's true speed

Her true speed x is within 2 mph of 56 mph.

This means the interval for x is
`56-2 \le \text{x} \le 56+2` which simplifies to
`54 \le \text{x} \le 58`

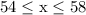
She could be going as slow as 54 mph, or as fast as 58 mph, or something in between.

The expression |x-56| measures the distance from x to 56 on the number line. Recall absolute value is used to ensure the distance isn't negative.

We want this distance to be within 2 units, i.e. we want the distance to be 2 or smaller.

`\text{distance on number line} \le 2\\\\|\text{x}-56| \le 2`

----------------

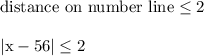
Here's what the steps look like to solve that absolute value inequality

`|\text{x}-56| \le 2\\\\-2 \le \text{x}-56 \le 2\\\\-2+56 \le \text{x}-56+56 \le 2+56\\\\54 \le \text{x} \le 58\\\\`

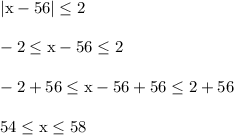
For the second step, we use the rule that |x| < k is the same as -k < x < k where k is some positive number.

In the third step, I added 56 to all three sides to isolate x fully.