Question

Find the LCM of n^3 t^2 and nt^4.

A) n 4t^6
B) n 3t^6
C) n 3t^4
D) nt^2

Answer 1

Answer: C) n 3t^4

Explanation:

Definition : The least common multiple (LCM) of any two expressions is the smallest expression that is divisible by both expressions.

Given expressions :
`n^3 t^2 \text{ and } nt^4`

Factorization form of
`n^3 t^2 \text{ and } nt^4` will be :

`n^3 t^2 =n* n* n* t* t`

tex]nt^4 =n \times t\times t\times t\times t[/tex]

The least common multiple of
`n^3 t^2 \text{ and } nt^4` :

`n^3 t^2 =n* n* n* t* t* t* t=n^3t^4`

Hence, the LCM of
`n^3 t^2 \text{ and } nt^4=n^3t^4`

Thus , the correct answer is option C).

Answer 2

The correct option is C.

Explanation:

The least common multiple (LCM) of any two numbers is the smallest number that they both divide evenly into.

The given terms are
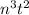`n^3t^2` and
`nt^4`.

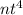The factored form of each term is

`n^3t^2=n* n* n* t* t`

`nt^4=n* t* t* t* t`

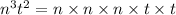
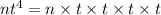
To find the LCM of given numbers, multiply all factors of both terms and common factors of both terms are multiplied once.

`LCM(n^3t^2,nt^4)=n* n* n* t* t* t* t`

`LCM(n^3t^2,nt^4)=n^3t^4`

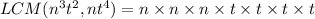
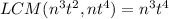
The LCM of given terms is
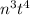`n^3t^4`. Therefore the correct option is C.