Question

Given sina=6/7 and cosb=-1/6, where a is in quadrant ii and b is in quadrant iii , find sin(a+b) , cos(a-b) and tan(a+b)

Answer 1

`\bf sin(a)=\cfrac{\stackrel{opposite}{6}}{\stackrel{hypotenuse}{7}} \\\\\\ \textit{using the pythagorean theorem}\\\\ c^2=a^2+b^2\implies \pm√(c^2-b^2)=a\qquad \begin{cases} c=hypotenuse\\ a=adjacent\\ b=opposite\\ \end{cases} \\\\\\ \pm√(7^2-6^2)=a\implies \pm√(13)=a \\\\\\ \textit{now, angle`

now, keep in mind that, the hypotenuse is just a radius unit, and thus is never negative, so if a fraction with it is negative, is the other unit. A good example of that is the second fraction here, -1/6, where the hypotenuse is 6, therefore the adjacent side is -1. Anyhow, let's find the opposite side to get the sin(b).


`\bf cos(b)=\cfrac{\stackrel{adjacent}{-1}}{\stackrel{hypotenuse}{6}} \\\\\\ \textit{using the pythagorean theorem}\\\\ c^2=a^2+b^2\implies \pm√(c^2-a^2)=b\qquad \begin{cases} c=hypotenuse\\ a=adjacent\\ b=opposite\\ \end{cases} \\\\\\ \pm√(6^2-(-1)^2)=a\implies \pm√(35)=a \\\\\\ \textit{now, angle`

now


`\bf \textit{Sum and Difference Identities} \\ \quad \\ sin({{ \alpha}} + {{ \beta}})=sin({{ \alpha}})cos({{ \beta}}) + cos({{ \alpha}})sin({{ \beta}}) \\ \quad \\ sin({{ \alpha}} - {{ \beta}})=sin({{ \alpha}})cos({{ \beta}})- cos({{ \alpha}})sin({{ \beta}}) \\ \quad \\ cos({{ \alpha}} + {{ \beta}})= cos({{ \alpha}})cos({{ \beta}})- sin({{ \alpha}})sin({{ \beta}}) \\ \quad \\ cos({{ \alpha}} - {{ \beta}})= cos({{ \alpha}})cos({{ \beta}}) + sin({{ \alpha}})sin({{ \beta}}) \\ \quad \\`


`\bf tan({{ \alpha}} + {{ \beta}}) = \cfrac{tan({{ \alpha}})+ tan({{ \beta}})}{1- tan({{ \alpha}})tan({{ \beta}})}\qquad tan({{ \alpha}} - {{ \beta}}) = \cfrac{tan({{ \alpha}})- tan({{ \beta}})}{1+ tan({{ \alpha}})tan({{ \beta}})}`


`\bf sin(a+b)=\cfrac{6}{7}\cdot \cfrac{-1}{6}+\cfrac{-√(13)}{7}\cdot \cfrac{-√(35)}{6}\implies \cfrac{-1}{7}+\cfrac{√(455)}{42} \\\\\\ \cfrac{-6+√(455)}{42}\\\\ -------------------------------\\\\ cos(a-b)=\cfrac{-√(13)}{7}\cdot \cfrac{-1}{6}+\cfrac{6}{7}\cdot \cfrac{-√(35)}{6}\implies \cfrac{√(13)}{42}-\cfrac{√(35)}{7} \\\\\\ \cfrac{√(13)-6√(35)}{42}`


`\bf -------------------------------\\\\ tan(a)=\cfrac{(6)/(7)}{-(√(13))/(7)}\implies -\cfrac{6}{√(13)}\implies -\cfrac{6√(13)}{13} \\\\\\ tan(b)=\cfrac{(-√(35))/(6)}{(-1)/(6)}\implies -√(35)\\\\ -------------------------------\\\\`


`\bf tan(a+b)=\cfrac{-(6)/(√(13))-√(35)}{1-\left( -(6)/(√(13)) \right)\left( -√(35) \right)}\implies \cfrac{(-6-√(455))/(√(13))}{1-(6√(35))/(√(13))} \\\\\\ \cfrac{(-6-√(455))/(√(13))}{(√(13)-6√(35))/(√(13))}\implies \cfrac{-6-√(455)}{√(13)-6√(35)}`

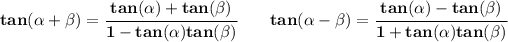
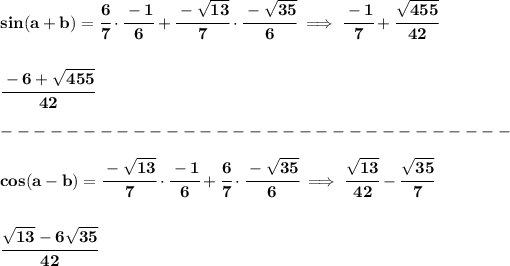
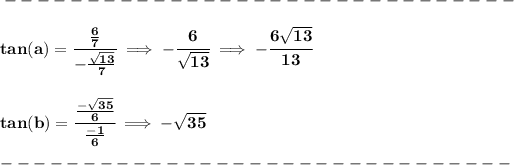
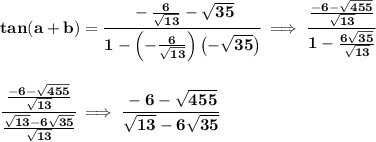
and now, let's rationalize the denominator of that one, hmmm let's see


`\bf \cfrac{-6-√(455)}{√(13)-6√(35)}\cdot \cfrac{√(13)+6√(35)}{√(13)+6√(35)} \\\\\\ \cfrac{-6√(13)-36√(35)-√(5915)-6√(15925)}{({√(13)-6√(35)})({√(13)+6√(35)})} \\\\\\ \cfrac{-6√(13)-36√(35)-13√(35)-210√(13)}{(√(13))^2-(6√(35))^2} \\\\\\ \cfrac{-216√(13)-49√(35)}{13-210}\implies \cfrac{-216√(13)-49√(35)}{-197} \\\\\\ \cfrac{216√(13)+49√(35)}{197}`