Question

How many real solutions does the system have Y=-3x-3 Y=x^2-3x+5

Answer 1

To find the solutions to each equation, we'll first have to set Y to 0. We have:
`-3x-3 &=0\\ x^2-3x+5=0`

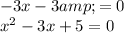
To obtain the solutions for both, you'll have to solve them for x. The first equation is linear, so obtaining a solution there is fairly straightforward, and you're guaranteed to get one real solution there. The second equation is a little more involved, and we'll need the quadratic formula to settle that one out. You might remember from earlier math classes that the quadratic formula gives you a way to quickly find the roots of a particular quadratic equation. Here's the full thing:


`x= (-b\pm√(b^2-4ac))/(2a)`

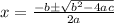
For the sake of this question, the only part we're concerned with is the
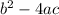
`b^2-4ac` bit, which is referred to as the descriminant of the quadratic. If
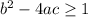
`b^2-4ac \geq 1`, we'll have two real solutions, since we'll need to evaluate the square root of the term for both positive and negative outcomes. If
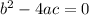
`b^2-4ac=0`, we only have one real solution, since adding and subtracting 0 from the
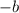
`-b` term have the same effect. If
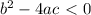
`b^2-4ac \ \textless \ 0`, we have no real solutions; the discriminant is nested inside a square root, and taking the square root of a negative number only produces imaginary results.

With that in mind, let's look at the discriminant of
`x^2-3x+5`.

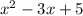
Looking at the coefficients and constant, we have a=1, b=-3, and c=5, which makes our discriminant


`(-3)^2-4(1)(5) = 9-20=-11`

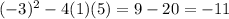
-11 is less than 0, so we have no real solutions to the second equation. This means that our first equation is the only one with a real solution, so the total number of real solutions for the system is 1.

Answer 2

Y = -3x-3 has one real solution.

Y= x^2 -3x + 5 has no real solutions because b^2 - 4ac, the discriminant, is less than zero.