What is the equation of the perpendicular to y=2/3x+1 that passes through the point (12,-6)

Question

asked Apr 23, 2018 44.1k views

1 Answer

Allenhwkim · Answer 1 · 2018-04-28T10:50:57+0000

well, first off let's check what is the slope of y = 2/3x+1.... .hmmmmm, notice
$\bf y=\stackrel{slope}{\cfrac{2}{3}}x+1$ , since the equation is already in slope-intercept form, we can see it has a slope of 2/3.

well then, a line perpendicular to that one, will have a negative reciprocal to it.

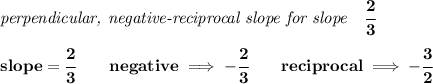
$\bf \textit{perpendicular, negative-reciprocal slope for slope}\quad \cfrac{2}{3}\\\\ slope=\cfrac{2}{{{ 3}}}\qquad negative\implies -\cfrac{2}{{{ 3}}}\qquad reciprocal\implies - \cfrac{{{ 3}}}{2}$

so, we're really looking for the equation of a line whose slope is -3/2 and goes through 12, -6.

$\bf \begin{array}{lllll} &x_1&y_1\\ % (a,b) &({{ 12}}\quad ,&{{ -6}}) \end{array} \\\\\\ % slope = m slope = {{ m}}= \cfrac{rise}{run} \implies -\cfrac{3}{2} \\\\\\ % point-slope intercept \stackrel{\textit{point-slope form}}{y-{{ y_1}}={{ m}}(x-{{ x_1}})}\implies y-(-6)=-\cfrac{3}{2}(x-12) \\\\\\ y+6=-\cfrac{3}{2}x+18\implies y=-\cfrac{3}{2}x+12$

What is the equation of the perpendicular to y=2/3x+1 that passes through the point (12,-6)

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

Please log in or register to add a comment.

No related questions found

Categories

Other Questions