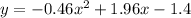Answer:
The standard form of a quadratic equation is given below as
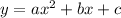
The y-intercept given is
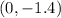
This indicates that at x=0, y= 1.4
Substitute x=0, y= 1.4 in the quadratic expression below
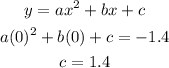
The x-intercept is given below as
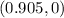
This means at x=0.905,y=0
Substitute x=0.905,y=0 in the quadratic expression above
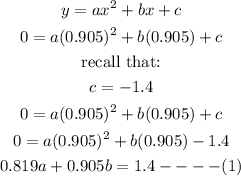
Since the third points below pass through the parabola, the third point is given below as

Substitute when x=3.07,y=0.314 in the quadratic expression above

Combine equations (1) and (2) and solve simultaneously
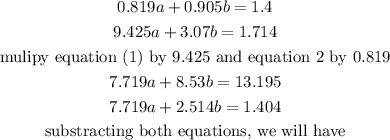
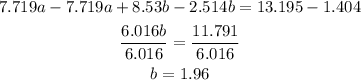
Substitute the value of b=1.96 in the equation (1)
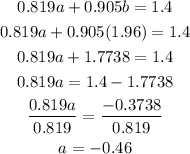
Hence,
The general equation will be