Question

regular polygons have congruent sides and congruent angles. The regular octagon has a perimeter represented by the expression shown perimeter equals 48 y - 40 write an expression to represent the length of one side of the Octagon ( the octagon has 8 equal sides )

Answer 1

Since we have a regular polygon, and it has congruent sides and angles, and we have that the perimeter (the sum of all of the sides of the regular polygon) is given by:

`P=48y-40`

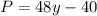
Then, each side of this octagon (it is a polygon with eight equal sides), is given by:

`s=(P)/(8)=((48y-40))/(8)\Rightarrow s=(48y)/(8)-(40)/(8)\Rightarrow s=6y-5`

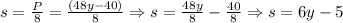
Therefore, the expression to represent the length of one side of the octagon is:

`s=6y-5`

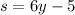
In summary, we divide the expression by 48y - 40 by 8 because each side of the octagon has the same length. Then, we divide 48y/8 = 6y, and -40/8= - 5, and the final expression is s = 6y -5 (the expression for each side of the octagon.)